【人気ダウンロード！】 3x y=10 x-y=2 elimination method 315742

 3x y = 10 By solving this equation by eliminating method y and y would get canceled, leaving 2x 3x = 5 10 5x = 15 x = 3 By putting value of x in equation 1, 2x y = 5 2 × 5 y = 5 y = 10 5 y = 5Get an answer for 'Solve the following system of equations 3x 4y = 25 2x y = 10' and find homework help for other Math questions at eNotesThe elimination method of solving systems of equations is also called the addition method To solve a system of equations by elimination we transform the system such that one variable "cancels out" Example 1 Solve the system of equations by elimination $$ \begin{aligned} 3x y &= 5 \\ x y &= 3 \end{aligned} $$

Pqs55atf8zl9hm

3x y=10 x-y=2 elimination method

3x y=10 x-y=2 elimination method-Free system of equations calculator solve system of equations stepbystep Asked by Pearlkaurvirk 9th Mar, 16, 0518 PM Expert Answer Solving 3x 4y =10 and 2x 2y =2 by elimination method Let 3x 4y =10 (1) and 2x 2y =2 (2) Multiply Equation (2) by 2 to make the coefficients of y equal Then we get the equation 4x – 4y = 4

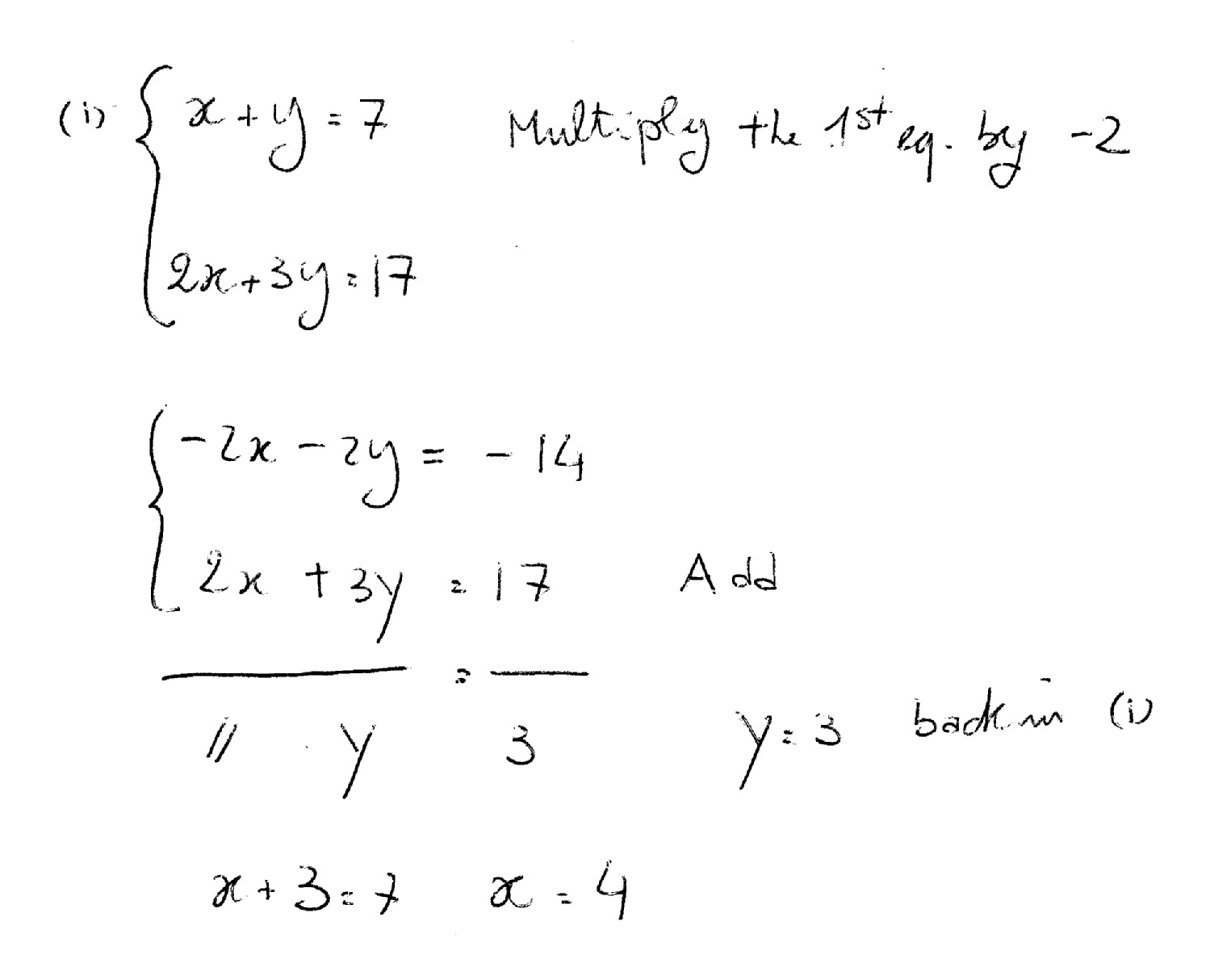
How Do You Solve The System Using The Elimination Method For X Y 7 And 2x 3y 17 Socratic

 Solve, using the method of substitution (i) 2x – 3y = 7;Solve the system by the elimination method 3x 2y 7 = 0 5x y 3 = 0 To eliminate y, the LCM is 2 Which of the following is the resulting equations? Simultaneous Linear Equation – Exercise 353 – Class IX Ashoora Arif Solve the following system of equations by the method of substitution (i) x y = 10 x – y = 12 (ii)3x – 7y = 7 11x 5y = 87 (iii) 3x – 4y = 10 4x 3y = 5

To practice more problems on the solutions of pair of linear equations by elimination method, download BYJU'S – The Learning App Ex 34, 1 (Elimination) Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 Solving (3) and (2) by Elimination –5y = –6 5y = 6 y = 𝟔/𝟓 Putting y = 6/5 in (1) x y = 5 x 6/5 = 5 x = 5 – 6/5 x = (5 × 5 − 6)/5 x = (25 −\\begin{aligned}&x2y=10\\&2xy=5\end{aligned}\ > <

Solve the system of linear equations using the GaussJordan elimination method 2x y – 2z = 1 x 3y z = 7 3x 4y z = 8 (X, Y, 2) =( Get more help from Chegg Solve it with our precalculus problem solver and calculator x 2y 5 3x 2 3y 10 solve by elimination method Mathematics TopperLearningcom dzs9yv22 Starting early can help you score better!X y = 2 y = x 2 2nd eq 3x y = 10y = 10 3x y = 3x 10;

X Y 6 X Y 2 By Elimination Method Novocom Top

Simultaneous Equations Gmat Math Study Guide

This video example shows how to solve systems of linear equations using Gaussian elimination method Initial problem is the following we need to solve the fHow to solve the following simultaneous equations?Elimination method First multiply one or both the equations by some suitable nonzero constants to make the coefficients of one variable numerically equal then add or subtract one equation from the other so that one variable gets eliminated (i) What is the Known?

X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube

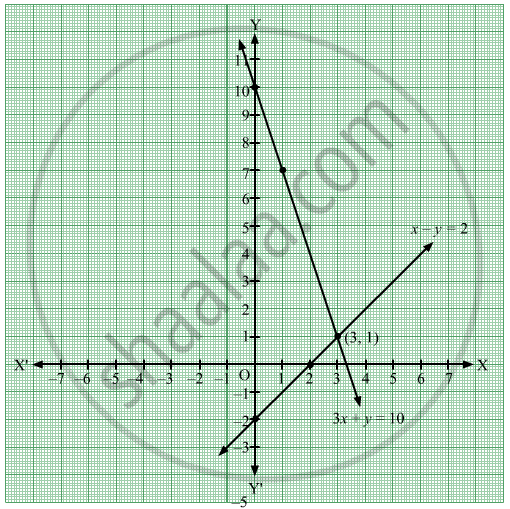
Solve The Following Simultaneous Equation Graphically 3x Y 10 X Y 2 Algebra Shaalaa Com

So you would have xx, which equals 2x yy=0(that is why they call it elimination) and 102, which =12 so since the y terms are eliminated we are left with 2x=12 take x's found value of 6 and plug it back into either equation I choose eq 2 6y=2y=4 solution(6,4) Solve using the elimination method Show your work If the system has no solution or an infinite number of solutions, state this 2x 6y = 12 x 3y = 3 3 Solve using the elimination method Show read moreSolve by Addition/Elimination xy=1 xy=3 Multiply each equation by the value that makes the coefficients of opposite Simplify Tap for more steps Simplify Tap for more steps Apply the distributive property Rewrite as Multiply Tap for more steps Multiply by Multiply by

Express Y In Terms Of X In The Expression 3x 7y 10

Please Solve Using Elimination Method Mathematics Topperlearning Com 5a5ymyhh

X – Y = 2However, there are several other ways to find the solution One is called the elimination method, where you add the two equations together, and if you can get one of the variables to add to zero, you have "eliminated" it So 2y 3x = 1 y 4x = 5 Rewriting so variables line up ***** 2y 3x = 12y 8x = 10 Mult by 2 So that 2y 2y = 0 *****11) − x = −y − 3 −6y − 3x = −9 12) −4 = −4y 4x −2y − 4x 2 = 0 13) 0 = x 2y 1 x = −y 14) 5 − 2y x = 0 6y = 12 3x4

The Elimination Method

Suppose That X Y And Z Are Positive Integers Such That Xy 6 Xz 10 And Yz 15 What Is The Value Of Xyz Quora

Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreEquation 1 3xy=10 Equation 2 2xy=5 There are 2 easiest and quickest ways to approach this question 1) By elimination When using the elimination method, you want to make sure that you choose the correct variable to eliminate to ensure only one variable (either x or y) is remained in theElimination method refers to the addition method of solving a set of linear equations This is quite similar to the method that you would have learned for solving simple linear equations Consider this example Consider a system x – 6 = −6 and x y = 8

Solve The Simultaneous Equations 10 X Y 2 X Y 4 15

For A Pair Of Equations 2x 3y 10 And 3x Y 4 Find X

Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method 3x−7y10=0;y−2x−3=0 Tiger Algebra SolverY = x 2 y = (4) 2 y = 4 2 y = 2 Enter 2 for y in the table, do the same for x=0 and x=4, you should get x y4 2 0 2 4 6 2nd eq (green) do the same in y = 3x 10 x y 2/3 3/2 3/2 User Determine if the solution set for the system of equations shown is the empty set, contains one point or is infinite x 2y = 0 2x 4y = 0 one solution no solution coincident Weegy Aone solution User 6x 2y = 5 3x y = 10 Solve the system of equations

Case Fiu Edu Mathstat Resources Math Help Math Help Pre Calculus Algebra Assets Lecture Notes Chapter 8 95blitzer Pdf

Solving A System Of Equations Using A Matrix Precalculus Socratic

 Alternately, subtract one equation form the other eliminating the x and allowing y=4 Given 1color(white)("XXX")xy=10 2color(white)("XXX")xy=2 Add 1 and 2 3color(white)("XXX")2x=12 rarr4color(white)("XXX")x=6 Subtract 2 from 1 5color(white)("XXX")2y=8 rarrcolor(white)("XXX")y=45x y = 9 (ii) 15x 01y = 62;The elimination method for solving systems of linear equations uses the addition property of equality You can add the same value to each side of an equation So if you have a system x – 6 = −6 and x y = 8, you can add x y to the left side of the first equation and add 8 to the right side of the equation And since x y = 8, you are adding the same value to each side of the first

X 4y 2 Solve For Y Novocom Top

5 1 Exercises 9

Answer to Solve by the elimination method 3x y = 1;Solve this linear system using the elimination method 3x – y = 3 x y = 17 Good heavens, the y's are already lined up and signed up for us to eliminate them (3x x) (y y) = (3 17) 4x = x = 5 Plug x = 5 into the second original equation and solve for y 5 y = 17 y = 12 The solution seems to be (5, 12) Let's make a quick check for body doubles, evil clones, or demonic3x 5y = 74 asked in Linear Equations by Anika01 ( 571k points) pair of linear equations in two variables

3x Y 10 X Y 2 Solve Graph Method Brainly In

Solving Systems Of Equations Using Elimination Ppt Download

Solve by the method of elimination (i) 2x – y = 3;Y has to be positive, mult eq by 1 1st eq (purple) as an example find y when x = 4, substituting for x in;(a) 2x 3y = 12(i) and x y = 1(ii) (ii)×3 ==> 3x 3y = 3(iii) Now we can eliminate y by adding (i) & (iii) (i) (iii) ==> 5x = 15 so x=3

J19

How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora

X 8y = 42 By signing up, you'll get thousands of stepbystep solutions to your homeworkSolve the following system of linear equations by elimination method 3x y = 8 , 5x y = 10 Solution 3x y = 8 (1) 5x y = 10 (2) The coefficients of y are same (1) (2)2x = 2 x = 1 By applying the value of x in (1), we get 3(1) y = 8 y = 8 – 3 y = 5 VerificationPractice Problems on Elimination Method Solve the system of linear equations using the elimination method 2x3y=6 and 2x5y=10;

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3

X Y 6 X Y 2 By Elimination Method Novocom Top

Solve each system using the elimination method 2x 3y7 x2y =7 2х 3), 3x 3y10 2x y 4 c) 3x 3y=6 2x4y 5 d) 2yx7 x3y=11 y2 15 a) b) e) 32 Solve each system x2y 3z = 3 b) 2x3yz 5 3x 3y 7z2 x2y5z 19 c) 2x3y 3z=15 5x4y2z 2 a) 3y 2z2 5z =The simultanous equation calculator helps you find the value of unknown varriables of a system of linear, quadratic, or nonlinear equations for 2, 3,4 or 5 unknowns A system of 3 linear equations with 3 unknowns x,y,z is a classic example This solve linear equation solver 3 unknowns helps you solve such systems systematicallyAbout Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding or subtracting your equations together You can use this Elimination Calculator to practice solving systems

7 Solve The Following System Of Linear Equations Chegg Com

A Solve The System Of Linear See How To Solve It At Qanda

Solve using the elimination method Show your work If the system has no solution or an infinite number of solutions, state this x y = 10 x – y = 2 algebra Solve using the elimination method Show your work If the system has no solution or an infinite number of solutions, state this 3x 6y = 3 / 6x 4y = 10 mathX2y=0,3xy=10 To solve a pair of equations using substitution, first solve one of the equations for one of the variables Then substitute the result for that variable in the other equation x2y=0 Choose one of the equations and solve it for x by isolating x on the left hand side of the equal sign Substitution method 1) The system of equations are y = 5y 1 and 2y 10 = 3 The above system of equations have only one variable that is y, so system of equations has no solution Solve the each equation separately for y Solve the equation 1 y = 5y 1 y 5y = 1 4y = 1 y = 1/4 Solve the equation 2 2y 10 = 3 2y = 3 10

Q Tbn And9gcsfztjretzfhrufhn2vvzlegsmmexxszfnttwkfemhx Q3xlfdr Usqp Cau

10 X Y 2 X Y 4 And 15 X Y 5 X Y 2 P S 1 4 Q2 Linear Equation In Two Variables Youtube

 Solve the system using elimination 10y − 2x = 50 6x − 3y = 12 A (5, 6) B (21, 02) C (21, 46) D (6, 5) math 3 Solve the following system using the elimination method 10x 6y = 16 5x 2y = 22 math Solve the system of equations by elimination (2 marks) y=2x^22x3Solve the following system using elimination method 2xy =−5 2 x y = − 5 3x−y =−10 3 x − y = − 10Avail 25% off on study pack

X Y 25 And X Y 5 What Is The Value Of X And Y Quora

Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y

 10/xy 2/xy=4_____(1) 15/xy5/xy=2_____(2) let 1/xy=A and 1/xy=Bua therefore eqn 1 and 2 will become 10B=4 15A5B=2 Now multiplying eqn 1 by 5 and eqn 2 by 2 we get 50A10B= 30A10B=4 Now by elimination method we have A=16/80=1/5 and B=1 but 1/xy=A and 1/xy =B putting the values of A and B we get xy=5____(3) and xy=1_____(4)Solve the Given equation in Elimination method and Substitution MethodSolve the following system of equations by elimination method 2x 3y = 46;

If X Y 10 And X Y 16 What Is The Value Of X Quora

4 3 Systems Of Linear Equations In Three Variables

 Solve the system using the elimination method 2x3y=17 3xy=15 Answered by a verified Math Tutor or Teacher We use cookies to give you the best possible experience on our website By continuing to use this site you consent to the use of cookies on your device as described in our cookie policy unless you have disabled themGauss Elimination Method Problems Solve the following system of equations using Gauss elimination method x y z = 9 2x 5y 7z = 52 2x y – z = 0 Solve the following linear system using Gaussian elimination method 4x – 5y = 6 2x – 2y = 1 Using Gauss elimination method3x 2y 7 = 0 5x y 3 = 0 3x 2y 7 = 0 10x 2y 6 = 0 3x 2y 7 = 0 10x 2y 6 = 0

If X Y 3 X Y 1 Then What Is X Y Quora

Solve Systems Of Equations Using Elimination Ppt Download

3x y = 7 Solution 2x – y = 3 (1) 3x y = 7 (2) The coefficient of y in the 1st and 2nd equation are same (1) (2) 2x – y = 3 3x y = 7 5x = 10 x = 10/5 = 2 By applying the value of x in (1), we getSolve Using Matrices by Elimination 2x3y=1 , 3xy=7 2x 3y = 1 2 x 3 y = 1 , 3x − y = 7 3 x y = 7 Write the system of equations in matrix form 2 3 1 3 −1 7 2 3 1 3 1 7 Row reduce Tap for more steps Perform the row operation R 1 = 1 2 R 1 R 1 = 1 2 R 1 on R 1 R 1 (row 1 1) in order to convert some elements in the row to 1 1\(x y = 5 \\2x 3 y= 4 \) Steps Elimination method

10 X Y 2 X Y 4 15 X Y 5 X Y 2 Solve By Elimination Brainly In

The Substitution Method

Solve the Following Simultaneous Equation Graphically3x Y = 10 ;3x – 04y = 112 asked in Algebra by nchi ( 4k points) algebra

Solving A System Of Equations Using A Matrix Precalculus Socratic

Solve 2xy X Y 3 2 Xy 2x Y 3 10 Mathematics Topperlearning Com X2oivz99

The Substitution Method

Hw 3 Due 9 27 Solve Each System Of Equations Chegg Com

3x 2y 17 2x Y 10 By Elimination Method Brainly In

Solve Each System Of Linear E See How To Solve It At Qanda

X3y10 X Y 2 2x Y 6 Xy3 X2y18 See How To Solve It At Qanda

Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 3

3 Systems Of Linear Equations

Maths Guru Please Help Me Solve This Simultaneous Equations For My Young Photo Education 2 Nigeria

If Math X Y 10 Math And Math X Y 12 Math Then What Are The Possible Values Of Math X Math And Math Y Math Quora

10 X Y 2 X Y 4 15

Q Tbn And9gcqj6i6ows0v3zqn94xovyirqjgvjrnzd94d7saosay5g M Vi4e Usqp Cau

How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora

Pqs55atf8zl9hm

Using The Elimination Method When Solving A System

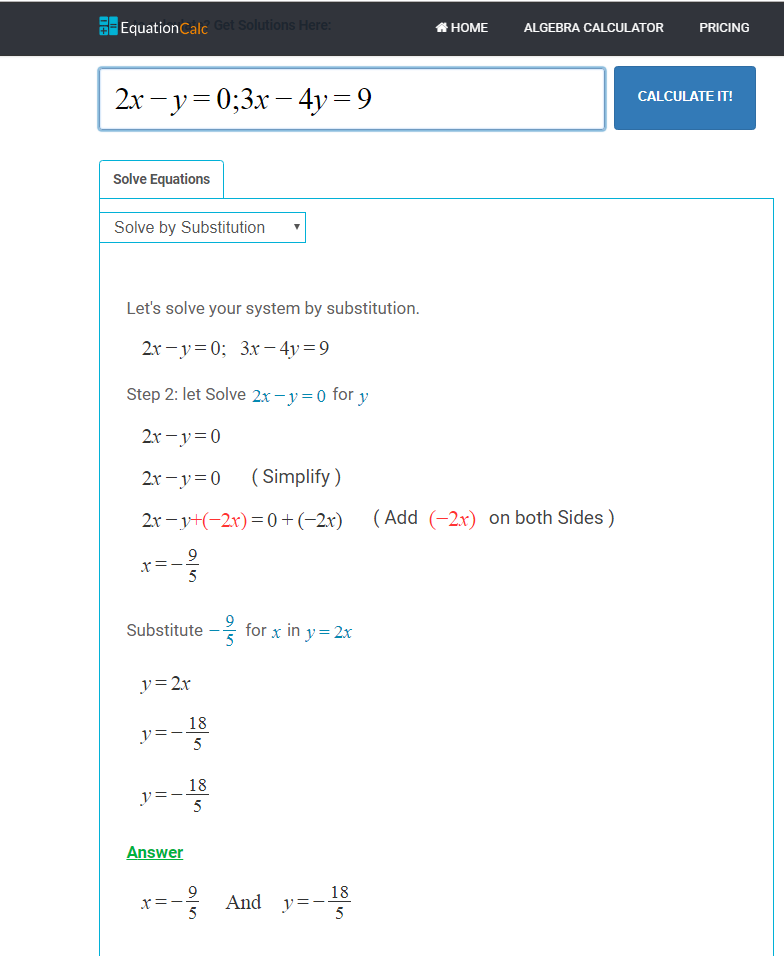
Simultaneous Equations Calculator With Steps

Solve By Reducing Them To A Pair Of Linear Equations 10 X Y 2 X Y 4 15 X Y 5 X Y 2 Youtube

X 1 2y 2 3x Y 1 Solve For X And Y By Elimination Process Brainly In

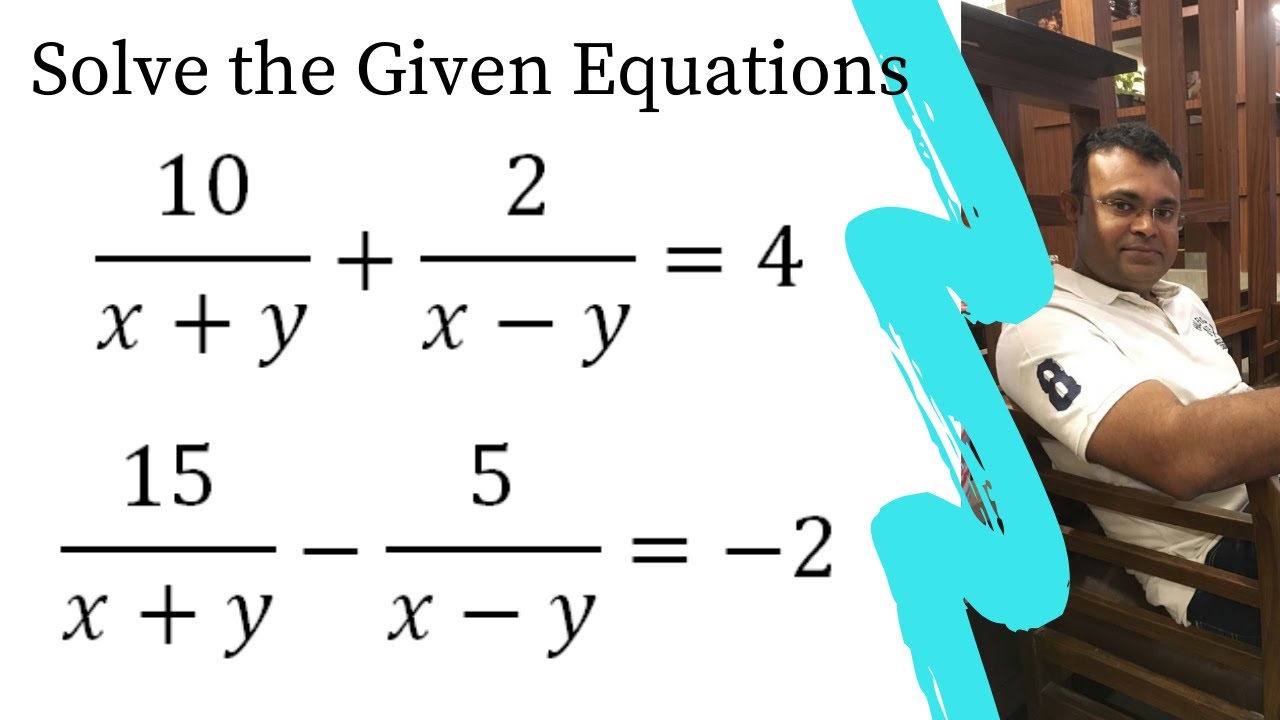
10 X Y 2 X Y 4 15 X Y 5 X Y 2 Solve The Pairs Of Equations By Reducing Them To A Pair Of Linear Youtube

3x Y 10 And X Y 2 Problem Set 1 Q3 5 Of Linear Equations In Two Variables Youtube

X Y 1 3x 2y 12 Novocom Top

Solve X Y 5 And 2x 2y 10 By Elimination Method Brainly In

Q Tbn And9gcq4veczzipyr Ffqkunhrw6gjd1yw8ock1fxwtna67kjb6rtcev Usqp Cau

Solve 3x 4y 10 2x 2y 2 By The Method Of Elimination

Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y

1 Find The General Solution Of Differential Equation Chegg Com

Better Form Of Displaying System Of Equations In An Enumerated List Tex Latex Stack Exchange

Use Elimination To Solve Each System Of Equations 1 Chegg Com

Www Marlboroschools Org Cms Lib Ny Centricity Domain 196 Integrated algebra Regents review Linear systems Solving systems by elimination Pdf

Systems Of Linear Equations

Ex 3 6 1 Vii And Viii Class 10 Ncert Solutions Maths

Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community

Systems Of Linear Equations Solving By Addition Elimination

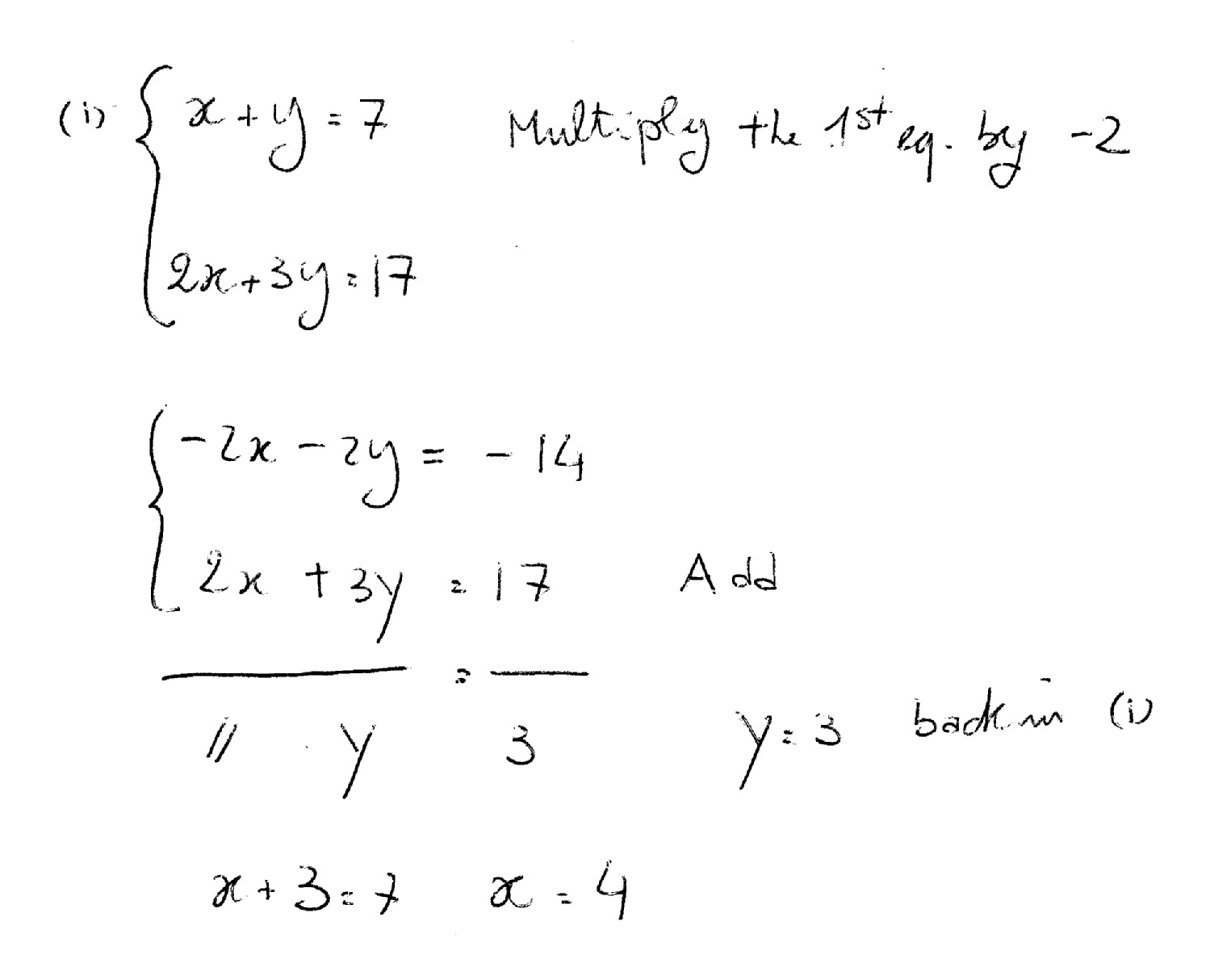
How Do You Solve The System Using The Elimination Method For X Y 7 And 2x 3y 17 Socratic

10 X Y 2 X Y 4 15 X Y 5 X Y 2 Solve Using Equation Reducible To A Pair Of Linear Equation In 2 Brainly In

Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt

Solve X Y 7 And 3x 2y 11

Chapter 9 Systems Of Linear Equations Pdf Free Download

Www Acpsd Net Cms Lib Sc Centricity Domain 21 7 3 Pdf

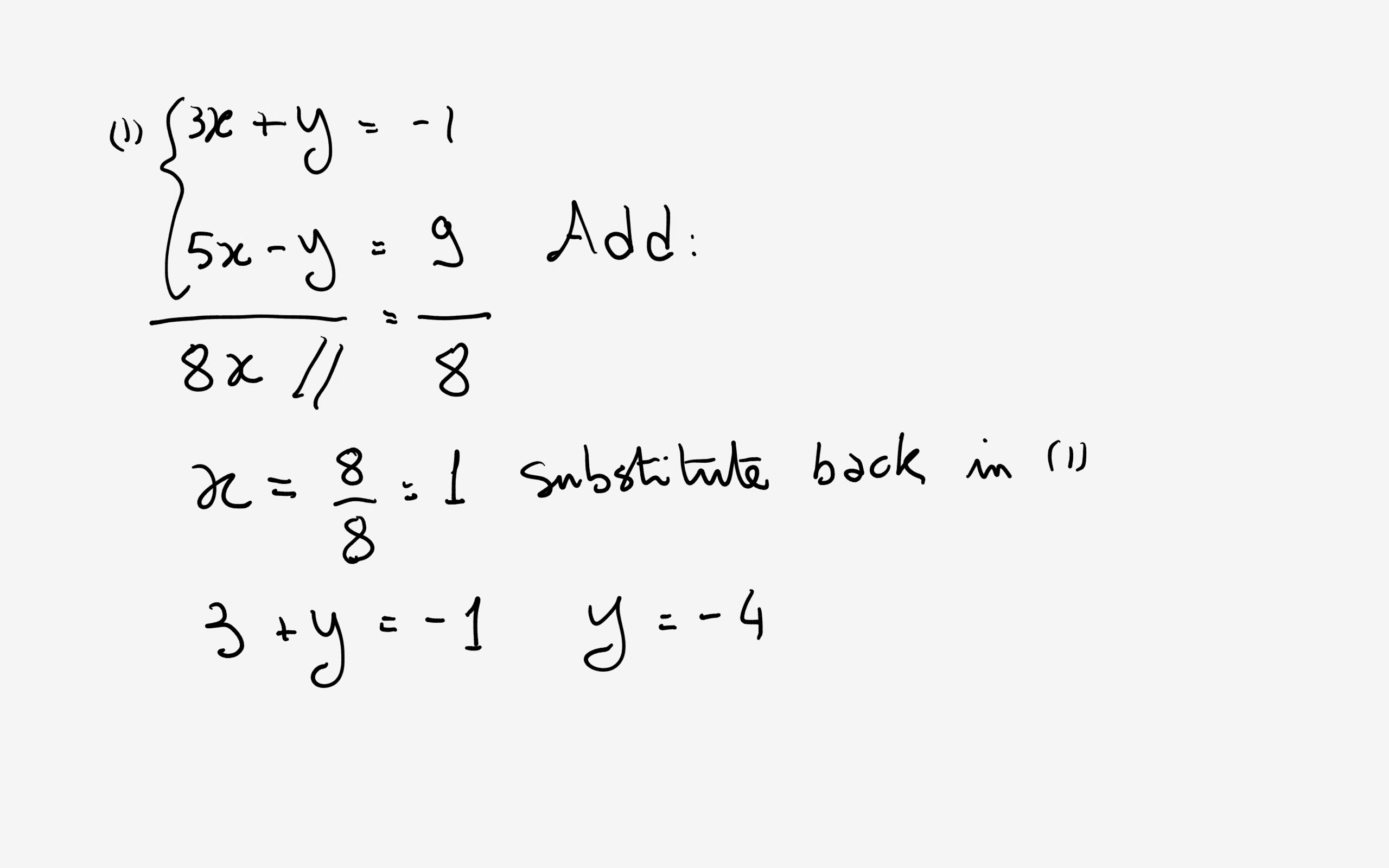
How Do You Solve The System Using The Elimination Method For 3x Y 1 And 5x Y 9 Socratic

Answered Find Any Four Ordered Triples That Saui Bartleby

Ex 3 6 1 Vii And Viii Class 10 Ncert Solutions Maths

Www Waynesville K12 Mo Us Cms Lib07 Mo Centricity Domain 603 A1 c6 l2 solution key worked out Pdf

Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15

Question 2 A Apply Gauss Elimination Method To Solve Chegg Com

6 2 Solving Systems Of Linear Equations 455 We Have Chegg Com

3x Y 10 X Y 2 In Graphical Method Brainly In

Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3

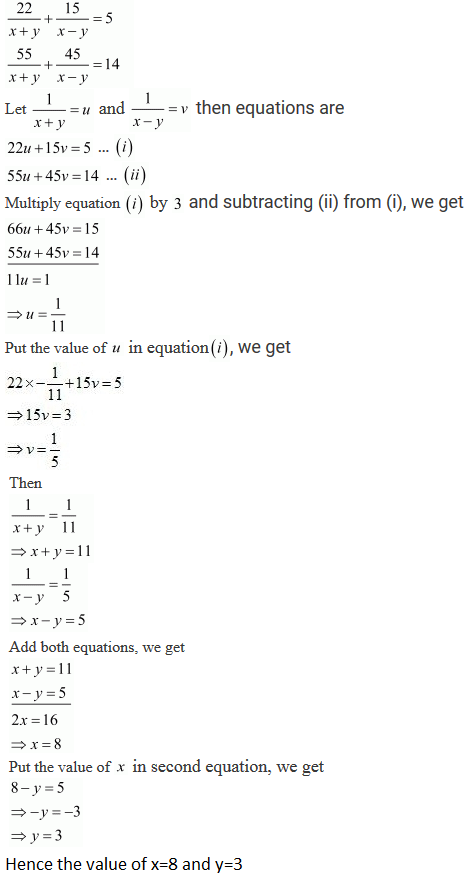
R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3

Solve By Substitution Method X Y 2 3x 2y 16 Brainly In

Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook

Systems Of Linear Equations Free Math Help

Solve X And Y X 6 Y 4 1 And 3x 4 X Y 2 7 4 Related Substitution Method Pair Of Linear Equations In Two Variables Edurev Class 10 Question

Solving Simultaneous Equations Equations And Inequalities Siyavula

Solve By Elimination Method 10 X Y 2 X Y 4 15 X Y 5 2 Y 2 Maths Pair Of Linear Equations In Two Variables Meritnation Com

Systems Of Equations With Substitution 2y X 7 X Y 4 Video Khan Academy

3x Y 10 X Y 2 Solve By Using Equating Coefficient Method Brainly In

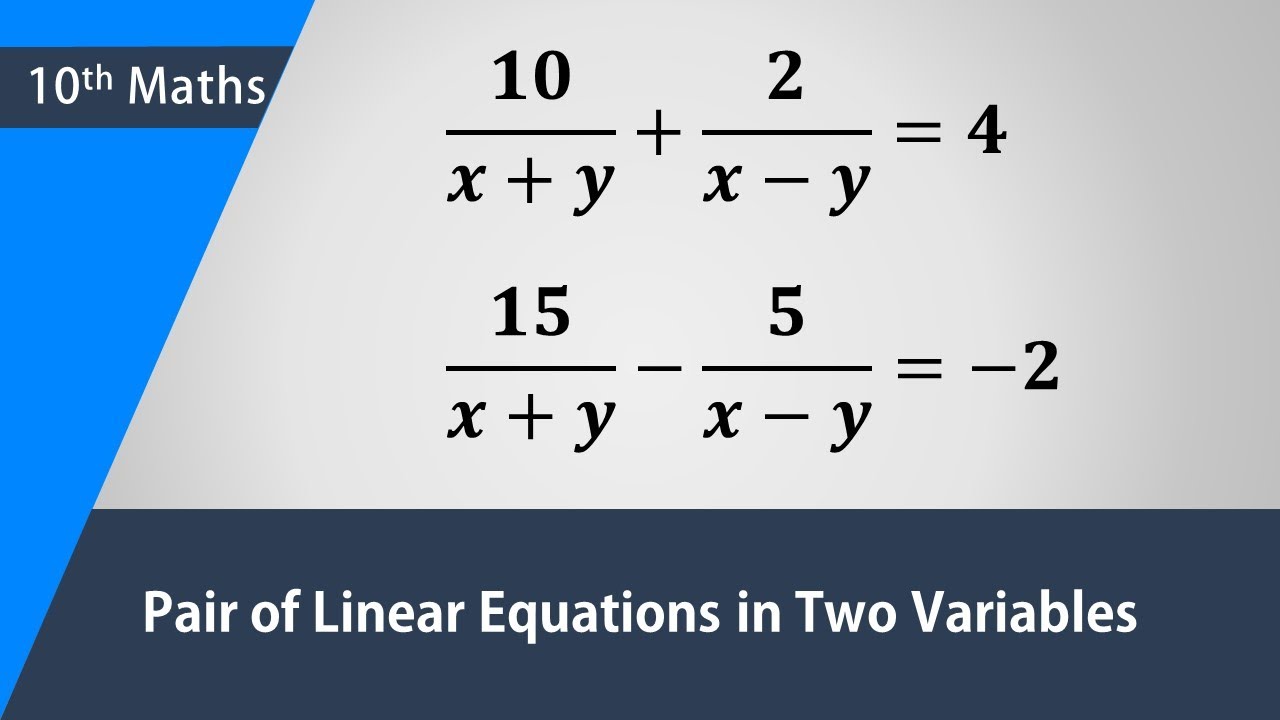
10 X Y 2 X Y 4 15 X Y 5 X Y 2 Solve For X And Y Youtube

3 Systems Of Linear Equations

Solve The Following System Of Linear Equations Graphically 3x Y 11 0 X Y 1 0 Sarthaks Econnect Largest Online Education Community

Www Waynesville K12 Mo Us Cms Lib07 Mo Centricity Domain 603 A1 c6 l2 solution key worked out Pdf

3x Y 10 X Y 2 Solve By Cramers Rule Brainly In

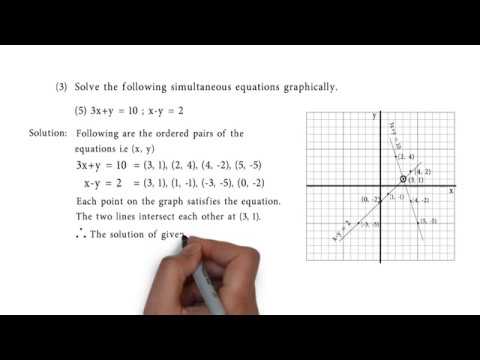
3x Y 10 And X Y 2 Problem Set 1 Q3 5 Of Linear Equations In Two Variables Youtube

3x Y 10 X Y 2 Solve Graph Method Brainly In

Solving A System Of Equations Using A Matrix Precalculus Socratic

X 2 Y 0 8 7 X Y 2 10 Pls Find The Answer For This In Elimination Method X 7 Y 3 5 X 2 Y 9 6find For This Also Rn Maths Pair Of Linear Equations In Two Variables Meritnation Com

Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook

X Y 6 X Y 2 By Elimination Method Novocom Top

X Y X Y 10 Solve The Following Brainly In

X Y 10 X Y 2 Cross Multiplication Elimination Substitution Brainly In